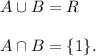Answer:
See explanation
Explanation:
1. R is the set of all integers with absolute value less than 10, thus
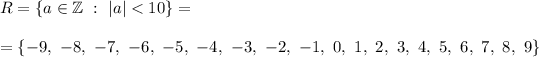
2. A is its subset containing all natural numbers less than 10, thus
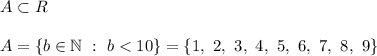
3. B is the set of all integer solutions of inequality 2x+5<9 that are less than 10 by absolute value (and therefore, it is also a subset of R). First, solve the inequality:
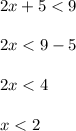
Thus,
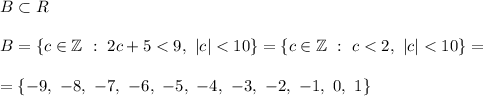
See the diagram in attached diagram.
Note that