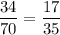Question

Please help me with probability!

Answer 1

What’s your question

Answer 2

The plate consists of 70 (7*10) squares with dimensions 1x1 square mm. Let
`w` be the number of white squares and
`b` the number of black squares. Then

`b+w=70`

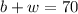
We're told there are 2 more black squares than white, so

`b=2+w`

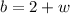
Then

`(2+w)+w=2+2w=70\implies1+w=35\implies w=34`

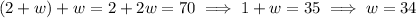
so there are 34 white squares and 36 black squares. The probability that Crystal is looking at a white square is

`(34)/(70)=(17)/(35)`