Question

Need this badly!!!!!!

Answer 1

Hello!

The answer is:

The center of the circle is located on the point (-9,-2) and the radius is 6 units.

Why?

To solve the problem, we need to use the given equation which is in the general form.

We are given the circle:

`x^(2)+y^(2)+18x+4y+49=0`

We know that a circle can be written in the following form:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

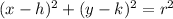
Where,

h is the x-coordinate of the center of the circle

k is the y-coordinate of the center of the circle

r is the radius of the circle.

So, to find the center and the radius, we need to perform the following steps:

- Moving the constant to the other side of the equation:

`x^(2)+y^(2)+18x+4y=-49`

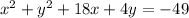
- Grouping the terms:

`x^(2)+18x+y^(2)+4y=-49`

- Completing squares for both variables, we have:

We need to sum to each side of the equation the following term:

`((b)/(2))^(2)`

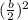
Where, b, for this case, will the coefficients for both terms that have linear variables (x and y)

So, the variable "x", we have:

`x^(2) +18x`

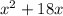
Where,

`b=18`

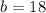
Then,

`((18)/(2))^(2)=(9)^(2)=81`

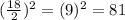
So, we need to add the number 81 to each side of the circle equation.

Now, for the variable "y", we have:

`y^(2) +4y`

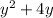
Where,

`b=4`

`((4)/(2))^(2)=(2)^(2)=4`

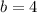
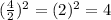
So, we need to add the number 4 to each side of the circle equation.

Therefore, we have:

`(x^(2)+18x+81)+(y^(2)+4y+4)=-49+81+4`

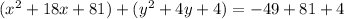
Then, factoring, we have that the expression will be:

`(x+9)^(2)+(y+2)^(2)=36`

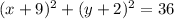
- Writing the standard form of the circle:

Now, from the simplified expression (after factoring), we can find the equation of the circle in the standard form:

`(x+9)^(2)+(y+2)^(2)=36`

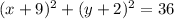
Is also equal to:

`(x-(-9))^(2)+(y-(-2))^(2)=36`

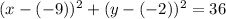
Where,

`h=-9\\k=-2\\r=√(36)=6`

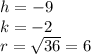
Hence, the center of the circle is located on the point (-9,-2) and the radius is 6 units.

Have a nice day!