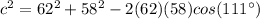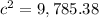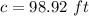Answer:
The distance between the two trees is
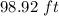
Explanation:
we know that
Applying the law of cosines
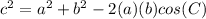
where
c -----> is the distance between the two trees
a ----> is the distance between the transit and the first tree
b ----> is the distance between the transit and the second tree
we have
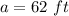
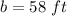
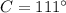
substitute and solve for c