Question

asked Oct 5, 2020 33.9k views

2 Answers

Jaeeun Lee · Answer 1 · 2020-10-06T01:34:56+0000

Hello!

The answer is:

The simplified expression is:

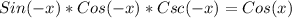
Sin(-x)*Cos(-x)*Csc(-x)=Cos(x)

To simplify the expression we need to use the following trigonometric identities:

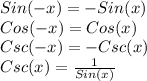
$Sin(-x)=-Sin(x)\\Cos(-x)=Cos(x)\\Csc(-x)=-Csc(x)\\Csc(x)=(1)/(Sin(x))$

We are given the expression:

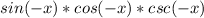
sin(-x)*cos(-x)*csc(-x)

So, applying the identities and simplifying, we have:

Sin(-x)*Cos(-x)*Csc(-x)=-Sin(x)*Cos(x)*-(1)/(Sin(x))

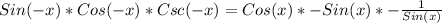
Sin(-x)*Cos(-x)*Csc(-x)=Cos(x)*-Sin(x)*-(1)/(Sin(x))

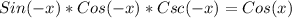
Sin(-x)*Cos(-x)*Csc(-x)=Cos(x)

Hence, the simplified expression is:

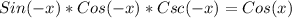
Sin(-x)*Cos(-x)*Csc(-x)=Cos(x)

Have a nice day!

Macro · Answer 2 · 2020-10-09T15:54:04+0000

Answer:

sin (-x) cos (-x) csc (-x) =cos(x)

Explanation:

We know by definition that the cosine is an even function, therefore

cos (-x) = cos (x)

We also know that the sin is an odd function, therefore

sin (-x) = -sin (x)

By definition:

cscx = (1)/(sinx).

Then:

csc(-x) = (1)/(sin(-x)).

csc(-x) = -(1)/(sin(x)).

Using these trigonometric properties we can simplify the expression

$sin (-x) cos (-x) csc (-x)= -sin(x)cos(x)*(-(1)/(sin(x)))\\\\sin (-x) cos (-x) csc (-x)=cos(x)$