Question

Find the limit of the function by using direct substitution. limit as x approaches zero of quantity x squared minus two.

Answer 1

`\lim_(x \to 0)\ x^2 -2 = -2`

Explanation:

We have the following limit

`\lim_(x \to 0)\ x^2 -2`

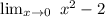
To solve this limit using direct substitution to substitute the value that tends x into f(x) and simplify.

In this case x tends to zero, then we substitute x = 0 in the function and simplify

`\lim_(x \to 0)\ x^2 -2= (0)^2 -2= -2`

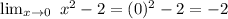
Therefore

`\lim_(x \to 0)\ x^2 -2 = -2`

When x approaches 0 then f(x) it tends to -2