Question

Write an equation with integer solutions of:

x = ±6, y = 0
and
x = 0, y = ±12

A)x2 + y2 + 6 = 0
B)4x2 + y2 + 144 = 0
C)x2 + y2 − 6 = 0
D)4x2 + y2 − 1

​

Answer 1

The correct answer is:

D. 4x2 + y2 − 1

`|Huntrw6|`

Answer 2

Answer: Option 'D' is correct.

Explanation:

Since we have given that

x = ±6, y = 0

and x = 0 and y = ±12

And we need an equation which has above as an integer solutions.

So, it becomes,

Consider
`4x^2+y^2-144=0`

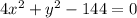
Put x = 0, we get

`0+y^2=144\\\\y^2=144\\\\y=√(144)\\\\y=\pm 12`

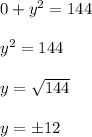
Similarly,

Put y = 0,

`4x^2+0=144\\\\4x^2=144\\\\x^2=(144)/(4)\\\\x^2=36\\\\\x=\pm 6`

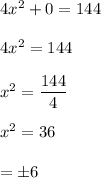
Hence, Option 'D' is correct.