Answer:
The position P is:
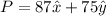 ft Remember that the position is a vector. Observe the attached image
ft Remember that the position is a vector. Observe the attached image
Explanation:
The equation that describes the height as a function of time of an object that moves in a parabolic trajectory with an initial velocity
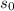 is:
is:
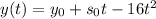
Where
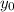 is the initial height = 0 for this case
is the initial height = 0 for this case
We know that the initial velocity is:
82 ft/sec at an angle of 58 ° with respect to the ground.
So:
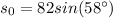 ft/sec
ft/sec
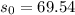 ft/sec
ft/sec
Thus
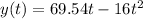
The height after 2 sec is:
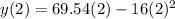

Then the equation that describes the horizontal position of the ball is
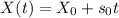
Where
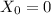 for this case
for this case
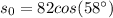 ft / sec
ft / sec
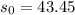 ft/sec
ft/sec
So
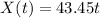
After 2 seconds the horizontal distance reached by the ball is:
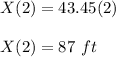
Finally the vector position P is:
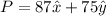 ft
ft