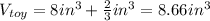Question

Find the volume of the toy rocket shown. The rocket consists of a prism and a pyramid

Answer 1

Answer:
`8.66in^3`

Explanation:

The oy rocket shown is formed by a rectangular prism and a regular pyramid whose base is a square.

The volume of the rectangular prism can be calculated with:

`V_(rp)=l*w*h`

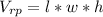
Where "l" is the length, "w" is the width and "h" is the height.

You can observe that:

`l=8in\\w=1in\\h=1in`

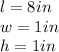
Then, you can substitute values:

`V_(rp)=(8in)(1in)(1in)=8in^3`

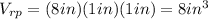
The volume of the regular square pyramid can be calculated with:

`V_p=(s^2*h)/(3)`

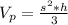
Where "s" is the lenght of a side of the base and "h" is the height of the pyramid.

You can observe in the figure that:

`s=1in\\h=2in`

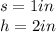
Substitute into the formula. Then:

`V_p=((1in)^2(2in))/(3)=(2)/(3)in^3`

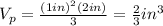
The volume of the toy rocket is the sum of the volume of the rectangular prism and the volume of the regular square pyramid. Then:

`V_(toy)=8in^3+(2)/(3)in^3=8.66in^3`