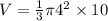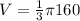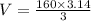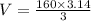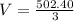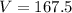Question

10 mm
4 mm
u What is the volume of the cone to the nearest whole number?
​

Answer 1

V=167.5 cubic mm

Explanation:

Volume of the Cone is given with the formula

`V=(1)/(3) \pi r^2h`

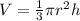
though we are not specified what is radius and which one is the height , we are assuming that ,

Height = 10 mm

Radius = 4 mm

Substituting these values in the formula we get

`V=(1)/(3) \pi 4^2 * 10`

`V=(1)/(3) \pi 160`

`V=(160 * 3.14)/(3)`

`V=(160 * 3.14)/(3)`

`V=(502.40)/(3)`

`V=167.5`