Answer:
options A and D are the correct options.
Explanation:
The parent exponential function is f(x) = 2ˣ
Now this function undergoes two transformations to form g(x) =
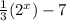
When parent function f(x) = 2ˣ is multiplied by
 , this means f(x) has been compressed vertically because
, this means f(x) has been compressed vertically because
 < 1.
< 1.
Now we subtract 7 from the new function

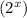 , that means we are shifting this function 7 units downwards on y-axis.
, that means we are shifting this function 7 units downwards on y-axis.
Therefore, options A and D are the correct options.