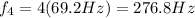Question

An organ pipe is 248 cm long.(a) Determine the fundamental overtone if the pipe is closed at one end.(b) Determine the first audible overtone if the pipe is closed at one end.(c) Determine the second audible overtone if the pipe is closed at one end.(d) Determine the third audible overtone if the pipe is closed at one end.(e) Determine the fundamental overtone if the pipe is open at both ends.(f) Determine the first audible overtone if the pipe is open at both ends.(g) Determine the second audible overtone if the pipe is open at both ends.(h) Determine the third audible overtone if the pipe is open at both end.

Answer 1

(a) 34.6 Hz

The fundamental frequency of a pipe closed at one end is given by

`f_1 = (v)/(4 L)`

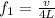
where

v = 343 m/s is the speed of the sound in air

L is the length of the pipe

In this problem,

L = 248 cm = 2.48 m

So, the fundamental frequency is

`f_1 = (343 m/s)/(4 (2.48 m))=34.6 Hz`

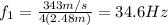
(b) 103.8 Hz

In a open-closed pipe, only odd harmonics are produced; therefore, the frequency of the first overtone (second harmonic) is given by:

`f_2 = 3 f_1`

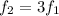
where

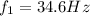`f_1 = 34.6 Hz` is the fundamental frequency.

Substituting into the equation,

`f_2 = 3 (34.6 Hz)=103.8 Hz`

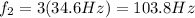
(c) 173 Hz

The frequency of the second overtone (third harmonic) is given by:

`f_3 = 5 f_1`

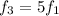
where

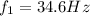`f_1 = 34.6 Hz` is the fundamental frequency.

Substituting into the equation,

`f_3 = 5 (34.6 Hz)=173 Hz`

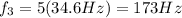
(d) 242.2 Hz

The frequency of the third overtone (fourth harmonic) is given by:

`f_4 = 7 f_1`

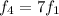
where

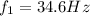`f_1 = 34.6 Hz` is the fundamental frequency.

Substituting into the equation,

`f_4 = 7 (34.6 Hz)=242.2 Hz`

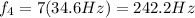
(e) 69.2 Hz

The fundamental frequency of a pipe open at both ends is given by

`f_1 = (v)/(2 L)`

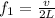
where

v = 343 m/s is the speed of the sound in air

L is the length of the pipe

In this problem,

L = 248 cm = 2.48 m

So, the fundamental frequency is

`f_1 = (343 m/s)/(2 (2.48 m))=69.2 Hz`

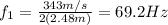
(f) 138.4 Hz

In a open-open pipe, both odd and even harmonics are produced; therefore, the frequency of the first overtone (second harmonic) is given by:

`f_2 = 2 f_1`

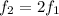
where

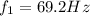`f_1 = 69.2 Hz` is the fundamental frequency.

Substituting into the equation,

`f_2 = 2 (69.2 Hz)=138.4 Hz`

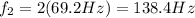
(g) 207.6 Hz

The frequency of the second overtone (third harmonic) in an open-open pipe is given by:

`f_3 = 3 f_1`

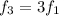
where

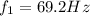`f_1 = 69.2 Hz` is the fundamental frequency.

Substituting into the equation,

`f_3 = 3 (69.2 Hz)=207.6 Hz`

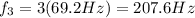
(h) 276.8 Hz

The frequency of the third overtone (fourth harmonic) in an open-open pipe is given by:

`f_4 = 4 f_1`

where

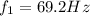`f_1 = 69.2 Hz` is the fundamental frequency.

Substituting into the equation,

`f_4 = 4 (69.2 Hz)=276.8 Hz`