Question

A mass moves back and forth in simple harmonic motion with amplitude A and period T.(a) In terms of A, through what distance does the mass move in the time T? ?A(b) Through what distance does it move in the time 5.00T? ?A(c) In terms of T, how long does it take for the mass to move through a total distance of 2A? ?T(d) How long does it take for the mass to move through a total distance of 7A? ?T(e) If the objects undergoes simple harmonic motion with a period T. In the time 5T/2 the object moves through a total distance of 16D. In terms of D, what is the object's amplitude of motion? ?D

Answer 1

(a) 4A

In a simple harmonic motion:

- The amplitude (A) is the maximum displacement of the system, measured with respect to the equilibrium position

- The period (T) is the time needed for one complete oscillation, so for instance is the time the system needs to go from position x=+A back to x=+A again

Therefore, we have that in one time period (1T) the distance covered is 4A. In fact, during one period (1T), the system:

- Goes from x=+A to x=0 (equilibrium position) --> distance covered: A

- Goes from x=0 to x=-A --> distance covered: A

- Goes from x=-A to x=0 (equilibrium position) --> distance covered: A

- Goes from x=0 to x=+A --> distance covered: A

So, in total, 4A.

(b) 20A

Since the system moves through a distance of 4A in a time interval of 1T, we can set a proportion to see what is the distance covered in the time 5.00 T:

`1 T : 4 A = 5T : d`

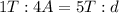
Solving for d, we find

`d=((4A)(5T))/(1 T)=20A`

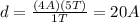
So, the distance covered in the time 5.00 T is 20 A.

(c) 0.5 T

Since the system moves through a distance of 4A in a time interval of 1T, we can set a proportion to see the time t that the system needs to move through a total distance of 2A:

`1 T : 4 A = t : 2A`

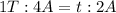
Solving for t, we find

`t=((2A)(1T))/(4 A)=0.5 T`

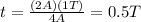
So, the time needed for the system to move through a total distance of 2A is 0.5T (half period).

(d) 7/4 T

As before, since the system moves through a distance of 4A in a time interval of 1T, we can set a proportion to see the time t that the system needs to move through a total distance of 7A:

`1 T : 4 A = t : 7A`

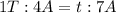
Solving for t, we find

`t=((7A)(1T))/(4 A)=(7)/(4)T`

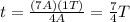
So, the time needed for the system to move through a total distance of 2A is 7/4 T

(e) 8/5 D

In a time of
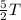`(5)/(2)T`, the distance covered is 16D.

We also now that the distance covered in 1T is 4A.

So we can find the distance covered in a time of
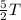`(5)/(2)T` in terms of A:

`1T:4A = (5)/(2)T:d\\d=((4A)((5)/(2)T))/(1T)=10A`

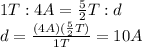
And we know that this distance must correspond to 16D, so we can find a relationship between A and D:

`10A=16D\\A=(16)/(10)D=(8)/(5)D`