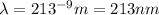Question

Electrons in a photoelectric-effect experiment emerge from a copper surface with a maximum kinetic energy of 1.10 eV. What is the wavelength of the light?

Answer 1

Answer: 213 nm

The photoelectric effect consists of the emission of electrons (electric current) that occurs when light falls on a metal surface under certain conditions.

If the light is a stream of photons and each of them has energy, this energy is able to pull an electron out of the crystalline lattice of the metal and communicate, in addition, a kinetic energy.

This is what Einstein proposed:

Light behaves like a stream of particles called photons with an energy

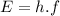`E=h.f` (1)

So, the energy
`E` of the incident photon must be equal to the sum of the Work function
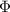`\Phi` of the metal and the kinetic energy
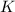`K` of the photoelectron:

`E=\Phi+K` (2)

Where
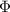`\Phi` is the minimum amount of energy required to induce the photoemission of electrons from the surface of a metal, and its value depends on the metal.

In the case of Copper
`\Phi=4.7eV`

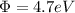
Now, applying equation (2) in this problem:

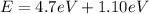`E=4.7eV+1.10eV` (3)

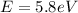`E=5.8eV` (4)

Now, substituting (1) in (4):

`h.f=5.8eV` (5)

Where:

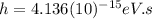`h=4.136(10)^(-15)eV.s` is the Planck constant

`f` is the frequency

Now, the frequency has an inverse relation with the wavelength
`\lambda`:

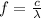`f=(c)/(\lambda)` (6)

Where
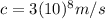`c=3(10)^(8)m/s` is the speed of light in vacuum

Substituting (6) in (5):

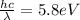`(hc)/(\lambda)=5.8eV` (7)

Then finding
`\lambda`:

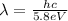`\lambda=(hc)/(5.8eV )` (8)

`\lambda=((4.136(10)^(-15) eV.s)(3(10)^(8)m/s))/(5.8eV )`

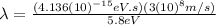
We finally obtain the wavelength:

`\lambda=213^(-9)m=213nm`