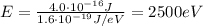(a)
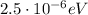
The energy of a photon is given by:
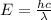
where
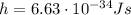 is the Planck constant
is the Planck constant
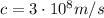 is the speed of light
is the speed of light
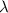 is the wavelength
is the wavelength
For the microwave photon,
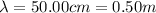
So the energy is
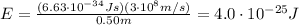
And converting into electronvolts,
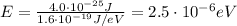
(b)
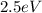
For the energy of the photon, we can use the same formula:
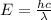
For the visible light photon,
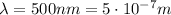
So the energy is
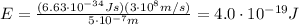
And converting into electronvolts,
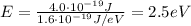
(c)
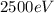
For the energy of the photon, we can use the same formula:
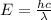
For the x-ray photon,
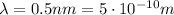
So the energy is
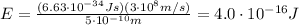
And converting into electronvolts,