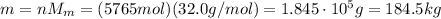1. 5765 mol
First of all, let's calculate the volume of the room (which corresponds to the volume of the gas):
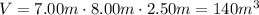
We also know the following data about the gas:
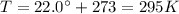 is the temperature
is the temperature
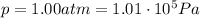 is the pressure
is the pressure
Then we can use the ideal gas law
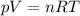
with R being the gas constant
to find the number of moles of the gas:
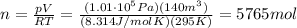
2. 184.5 kg
The molar mass of oxygen is
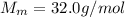
this corresponds to the mass of 1 mol of oxygen.
In this problem, the number of moles is
n = 5765 mol
So the total mass of these n moles of oxygen will be: