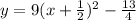Answer:
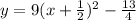
Explanation:
An equation in the vertex form is written as
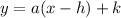
Where the point (h, k) is the vertex of the equation.
For an equation in the form
 the x coordinate of the vertex is defined as
the x coordinate of the vertex is defined as
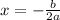
In this case we have the equation
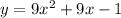 .
.
Where
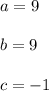
Then the x coordinate of the vertex is:
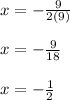
The y coordinate of the vertex is replacing the value of
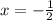 in the function
in the function
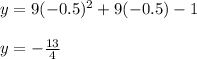
Then the vertex is:
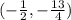
Therefore The encuacion excrita in the form of vertice is:
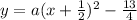
To find the coefficient a we substitute a point that belongs to the function
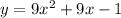
The point (0, -1) belongs to the function. Thus.
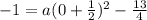
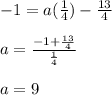
Then the written function in the form of vertice is