Question

The amplitude of a system moving in simple harmonic motion is doubled. Determine by what factor the following change.

(a) the total energy
(b) the maximum speed
(c) the maximum acceleration
(d) the period

Answer 1

(a) The total energy increases by a factor 4

The total energy of a simple harmonic system is given by:

`E=(1)/(2)kA^2`

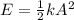
where

k is the spring constant

A is the amplitude of the motion

In this part of the problem, the amplitude is doubled:

A' = 2A

So the new total energy is

`E=(1)/(2)k(A')^2=(1)/(2)k(2A)^2=4((1)/(2)kA^2)=4E`

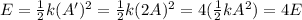
So, the energy quadruples.

(b) The maximum speed increases by a factor 2

The maximum speed in a simple harmonic motion is given by

`v=\omega A`

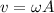
where

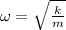`\omega=\sqrt{(k)/(m)}` is the angular frequency, with k being the spring constant and m the mass

A is the amplitude

In this part of the problem, k and m do not change, so the angular frequency does not change. Instead, the amplitude is doubled:

A' = 2A

So the new maximum speed is

`v'=\omega (A')=\omega (2A)=2 (\omega A)=2 v`

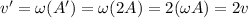
so, the maximum speed doubles.

(c) The maximum acceleration increases by a factor 2

The maximum acceleration in a simple harmonic motion is given by

`a=\omega^2 A`

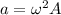
where

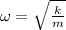`\omega=\sqrt{(k)/(m)}` is the angular frequency, with k being the spring constant and m the mass

A is the amplitude

In this part of the problem, k and m do not change, so the angular frequency does not change. Instead, the amplitude is doubled:

A' = 2A

So the new maximum acceleration is

`a'=\omega^2 (A')=\omega^2 (2A)=2 (\omega^2 A)=2 a`

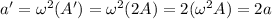
so, the maximum acceleration doubles.

(d) The period does not change

The period in a simple harmonic motion is given by

`T=2\pi \sqrt{(m)/(k)}`

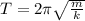
where m is the mass and k is the spring constant.

In this problem, the amplitude is doubled:

A' = 2A

However, we notice that the period does not depend on the amplitude, and since both m and k do not change, then the period will remain constant.