Answer: Option B
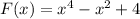
Explanation:
We have the function
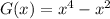 and we know that it contains the point (0,0). That is, it cuts the y axis and y = 0
and we know that it contains the point (0,0). That is, it cuts the y axis and y = 0
Then the graph of F(x) is shown in the image and we know that it is a transformation of F(x).
The function F(x) cuts the y axis and y = 4.
For this reason we can conclude that the function F(x) is the function G(x) displaced 4 units upwards.
The transformation that shifts the graph of a function k units upwards is:
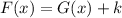
Where
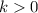 .
.
In this case k = 4. Therefore:
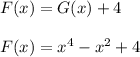
The answer is Option B