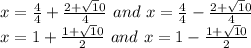Question

Using the quadratic formula to solve 2x^2 = 4x - 7, what are the values of x?

Answer 1

The values of x are
`x= 1+(1+\sqrt10)/(2) \,\,and \,\, x= 1-(1+\sqrt10)/(2)`

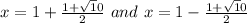
Explanation:

The quadratic formula is:

`x=(-b\pm√(b^2-4ac))/(2a)`

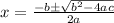
Our equation is:

`2x^2 = 4x -7\\2x^2-4x+7=0`

a= 2, b= -4 and c =7

Putting the values in quadratic formula:

`x=(-(-4)\pm√((-4)^2-4(2)(7)))/(2(2))\\x=(4\pm√(16-56))/(4)\\x=(4\pm√(-40))/(4)`

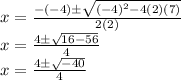
Since we have -40 in the under root we will find its factors and simplify:

Factors of 40 = 2*2*2*5

`x=(4\pm√(2*2*2*5))/(4)\\x=(4\pm√(2^2 *2*5))/(4)\\x=(4\pm√(2^2)√(2*5))/(4)\\x=(4\pm2√(10))/(4)\\x=(4+2√(10))/(4) \,\, and \,\, x=(4-2√(10))/(4)`

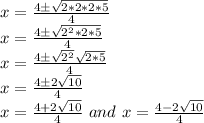
The values of x are:

`x=(4+2√(10))/(4) \,\, and \,\, x=(4-2√(10))/(4)`

`x= (4)/(4)+ (2+\sqrt10)/(4) \,\,and \,\, x= (4)/(4)- (2+\sqrt10)/(4)\\x= 1+(1+\sqrt10)/(2) \,\,and \,\, x= 1-(1+\sqrt10)/(2)`