Question

Given the equation of a circle, determine the center and the radius.〖(x+5)〗2+〖(y-1)〗2=9.

The equation of a circle is (x-h)2 +(y-k)2 = r2

Answer 1

Hello!

The answer is:

The center of the circle is located on the point (-5,1) and the radius is equal to 3 units.

Why?

To determine the center and the radius of a circle from its equation, we need to look for "h" and "k", being "h" the x-coordinate of the center and "k" the y-coordinate the center, then, calculate the radius.

Since we are given the ordinary equation of the circle, we can find the radius and the center directly.

The ordinary equation is:

`(x-h)^(2) +(y-k)^(2) =r^(2)`

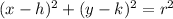
Where,

h is the x-coordinate of the center

y is the y-coordinate of the center

r is the radius.

So, we are given the circle:

`(x+5)^(2) +(y-1)^(2) =9`

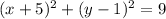
Which is also equal to:

`(x-(-5))^(2) +(y-(1))^(2) =9`

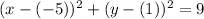
Where,

`h=-5\\k=1`

`r^(2)=9\\\sqrt{r^(2)}=√(9) \\r=3units`

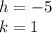
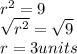
Hence, the center of the circle is located on the point (-5,1) and the radius is equal to 3 units.

Have a nice day!

Answer 2

The center is (-5,1)

and

the radius is 3

Explanation:

The given equation of the circle is

`(x+5)^2+(y-1)^2=9`

We can rewrite this equation in the form;

`(x-h)^2+(y-1)^2=r^2`

This implies that;

`(x--5)^2+(y-1)^2=3^2`

When we compare, we get;

(h,k)=(-5,1) which is the center and r=3 the radius.