For this case we must simplify the following expression:
![\frac {6-3 \sqrt [3] {6}} {\sqrt [3] {9}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mxo0onow94x8dlifmoglaq93ut0sxe48jo.png)
Multiplying the numerator and denominator by
![(\sqrt [3] {9}) ^ 2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z0jw0rrlfcyl4onn5eetj7h056gkpyekoj.png)
![\frac {6-3 \sqrt [3] {6}} {\sqrt [3] {9}} * \frac {(\sqrt [3] {9}) ^ 2} {(\sqrt [3] { 9}) ^ 2} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/u29sjh4pov3nyskd9axuuv4gf46nkal9qe.png)
We rewrite:
![\frac {\frac {6-3 \sqrt [3] {6}} * (\sqrt [3] {9}) ^ 2} {\sqrt [3] {9} * (\sqrt [3] {9 }) ^ 2} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/g859sgn9qq4si3vsz2etp3staaczutvgtc.png)
By properties of powers we have that:
![a ^ m * a ^ n = a ^ {m + n}\\\frac {(6-3 \sqrt [3] {6}) * (\sqrt [3] {9}) ^ 2} {(\sqrt [3] {9}) ^ 3} =\\\frac {(6-3 \sqrt [3] {6}) * (\sqrt [3] {9}) ^ 2} {9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/eb6l96xzjqyd69dv1a74refgt0t4ny8kp5.png)
We rewrite, moving the exponent within the radical:
![\frac {(6-3 \sqrt [3] {6}) * \sqrt [3] {9 ^ 2}} {9} =\\\frac {(6-3 \sqrt [3] {6}) * \sqrt [3] {81}} {9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ixwu11m06ihmsixfjjj4f037764qjdo144.png)
We can rewrite
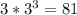
![\frac {(6-3 \sqrt [3] {6}) * \sqrt [3] {3 * 3 ^ 3}} {9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qjgj0sbk0dnyurki28ffyu6xuvj90p2yo5.png)
We simplify:
![\frac {(6-3 \sqrt [3] {6}) * 3 \sqrt [3] {3}} {9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dq2yv9raxeom2dwh45zd17qwq2zkfo1m8b.png)
We apply distributive property:
![\frac {18 \sqrt [3] {3} -9 \sqrt [3] {18}} {9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/b4n52jei55wk8qj8nixde6bw65bonip5o3.png)
Simplifying we finally have:
![2 \sqrt [3] {3} - \sqrt [3] {18}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/abuma03c6vcxb1yz5itfyws7zd3uliz133.png)
Answer:
![2 \sqrt [3] {3} - \sqrt [3] {18}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/abuma03c6vcxb1yz5itfyws7zd3uliz133.png)