Question

1. By what factor will the Electrostatic Force between two charged objects change when the amount of charge on ONE object doubles?

A. 2
B. 4
C. 1/2
D. 1/4
2. By what factor will the Electrostatic Force between two charged objects change when the distance between the TWO charged objects doubles?
A. 2
B. 4
C. 1/2
D. 1/4
3. By what factor will the Electrostatic Force between two charged objects change when the amount of charge on both objects doubles AND the distance between the two charged objects triples?
A. 2/3
B. 3/4
C. 2/9
D. 2/9

Answer 1

1) A. 2

The electrostatic force between two objects is given by:

`F=k(q_1 q_2)/(r^2)`

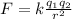
where

k is the Coulomb's constant

q1 and q2 are the charges of the two objects

r is the separation between the two objects

In this problem, the charge of one object is doubled, so

`q_1' = 2q_1`

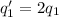
Therefore the new force is

`F'=k(q_1' q_2)/(r^2)=k((2q_1)q_2)/(r^2)=2((kq_1 q_2)/(r^2))=2F`

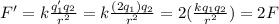
So, the force will double.

2) D. 1/4

Using the same formula, the electrostatic force between the two objects is:

`F=k(q_1 q_2)/(r^2)`

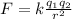
In this problem, the distance between the two objects is doubled, so

`r' = 2r`

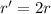
Therefore the new force is

`F'=k(q_1 q_2)/((r')^2)=k(q_1 q_2)/((2r)^2)=(1)/(4)((kq_1 q_2)/(r^2))=(F)/(4)`

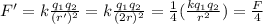
So, the force will decrease to 1/4 of its original value.

3) 4/9

Using the same formula, the electrostatic force between the two objects is:

`F=k(q_1 q_2)/(r^2)`

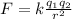
In this problem, the amount of charge on both objects doubles, so

`q_1' = 2q_1`

`q_2' = 2q_2`

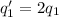
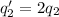
Also, the distance is tripled

`r' = 3r`

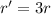
Therefore the new force is

`F'=k(q_1' q_2')/((r')^2)=k((2q_1) (2q_2))/((3r)^2)=(4)/(9)((kq_1 q_2)/(r^2))=(4)/(9)F`

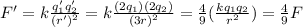
So, the force will decrease to 4/9 of its original value.