Question

What is the area of the rectangle shown on the coordinate plane?

Enter your answer in the box. Do not round at any steps.

Answer 1

Aswer:

The area of the rectangle is 12 sq. units

Explanation:

From the question :

we first find the length and width of the rectangle using the distance formula.

For the length we use the points

(-1,-2) and (-4,1)

`l = \sqrt{( {x - x_1)}^(2) + ( {y - y_1)}^(2) }`

`l = \sqrt{( { - 1 - ( - 4))}^(2) +{(-2 - 1)}^(2) }`

`l = \sqrt{{3}^(2) +{( - 3)}^(2)}`

`l = √(9 + 9)`

`l = √(18) = 3√(2) \: units`

For the width, let us take the points (-6,-1) and (-4,1)

`w = \sqrt{ {( - 6 - ( - 4))}^(2) + {(-1 - 1) }^(2) }`

`w = \sqrt{ {2}^(2) + {( - 2)}^(2) }`

`w = √(4+4)`

`w = √(8 ) = 2 √(2) \: units`

The area of the rectangle

`= l * w`

`A = 3 √(2) * 2√(2)`

`A = 3 * 2 * 2`

`A =12 \: sq.units`

Answer 2

Hello!

The answer is:

The area of the rectangle is equal to
`12units^(2)`

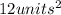
Why?

To find the area of the rectangle shown on the coordinate plan, first, we need to calculate the distance between the points that conforms two of the sides of the rectable (base and height).

We can use any of the four vertex points shown on the coordinate plane, so, we will use the points:

1 - (-4,1)

2 - (-1,-2)

3 - (-3,-4)

Then, calculating the length of the sides, we have:

Base:

`Base=distance(FirstPoint,SecondPoint)=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)`

`Base=\sqrt{(-1-(-4))^(2)+(-2-1)^(2)}\\\\Base=\sqrt{(3)^(2)+(-3)^(2)}\\\\Base=√((9+9))=√(18)units`

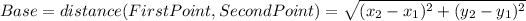
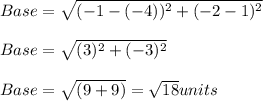
Height:

`Height=distance(SecondPoint,ThirdPoint)=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)`

`Height=\sqrt{(-3-(-1))^(2)+(-4-(-2))^(2)`

`Height=\sqrt{(-2)^(2)+(-2)^(2)`

`Height=√(4+4)`

`Height=√(8)units`

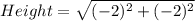
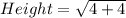
Therefore, calculating the are of the rectangle, we have:

`Area=base*height\\\\Area=√(18unis)*√(units)=√(144)=12units^(2)`

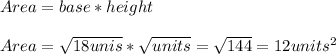
Hence, the area of the rectangle is equal to
`12units^(2)`

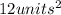
Have a nice day!