For this case we have the
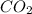
It is composed of one atom of carbon and two of oxygen.
The atomic mass of carbon and oxygen, which can be found in a periodic table, are given by:

Then, we find the atomic mass of
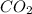 :
:
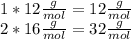
Adding we have:

To find the percentage of oxygen, we divide the atomic mass of the two oxygen atoms between that of
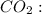
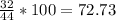 %
%
Thus, the percentage of oxygen is 72.73%
Answer:
72.73%