Question

The measure of a vertex angle of an isosceles triangle is 120° and the length of a leg is 8 cm. Find the length of a diameter of the circle circumscribed about this triangle.

Answer 1

The length of a Diameter is 3.714

EXPLANATION

The circumscribed triangle is shown in the attachment.

We use the cosine ratio to find the altitude of the isosceles triangle.

`\cos(60 \degree) = (altitude)/(hypotenuse)`

`\cos(60 \degree) = (altitude)/(8)`

Altitude =8cos(60°)

Altitude=4cm

Let the upper half of the altitude be y cm.

Then the radius of the circle is (y-4)cm

The upper radius meets the tangent at right angles.

From the smaller right triangle,

`\sin(60 \degree) = (4 - y)/(y)`

`y\sin(60 \degree) = 4 - y`

`y\sin(60 \degree) + y= 4`

`(\sin(60 \degree) + 1)y= 4`

`y= (4)/(\sin(60 \degree) + 1)`

`y = 16 - 8 √(3)`

y=1.857

The diameter is 2y

`d = 32 - 16 √(3)`

=2(1.875)

The length of a Diameter is 3.714

Answer 2

Diameter of the circle is 16 cm.

Explanation:

Given : The measure of a vertex angle of an isosceles triangle is 120° and the length of a leg is 8 cm.

To find : The length of a diameter of the circle circumscribed about this triangle?

Solution :

We construct a circle in which an ABC isosceles triangle is formed.

Refer the attached figure below.

The measure of a vertex angle of an isosceles triangle is 120° .

The length of a leg is 8 cm, AC=8 cm

Vertex angle is divided by the line touching the center of the circle.

So,
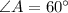`\angle A=60^\circ` and line AD=radius of the circle

Applying property of isosceles triangle,

Now, ∠DAC=∠ACD=∠CDA=60°

AC=DC=8 cm

The radius of the circle is 8 cm.

The diameter of the circle is twice the radius.

Therefore, The diameter of the circle is d=2(8)=16 cm.