Question

Calculate the energy of a photon having a wavelength in thefollowing ranges.

(a) microwave, with λ = 50.00 cm
eV
(b) visible, with λ = 500 nm
eV
(c) x-ray, with λ = 0.50 nm
eV

Answer 1

Answers:

The energy
`E` of a photon is given by the following formula:

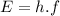`E=h.f` (1)

Where:

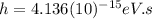`h=4.136(10)^(-15)eV.s` is the Planck constant

`f` is the frequency

Now, the frequency has an inverse relation with the wavelength
`\lambda`:

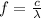`f=(c)/(\lambda)` (2)

Where
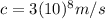`c=3(10)^(8)m/s` is the speed of light in vacuum

Substituting (2) in (1):

`E=(hc)/(\lambda)` (3)

Knowing this, let's begin with the answers:

(a) Microwave: 50.00 cm

For
`\lambda=50cm=0.5m`

`E=((4.136(10)^(-15) eV.s)(3(10)^(8)m/s))/(0.5m)`

`E=(1.24(10)^(-6)eV.m )/(0.5m)`

`E=2.48(10)^(-6)eV`

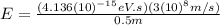
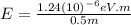
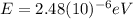
(b) Visible: 500 nm

For
`\lambda=500nm=500(10)^(-9)m`

`E=((4.136(10)^(-15) eV.s)(3(10)^(8)m/s))/(500(10)^(-9)m)`

`E=(1.24(10)^(-6)eV.m )/(500(10)^(-9)m)`

`E=2.48 eV`

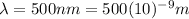
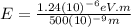
(c) X-ray: 0.5 nm

For
`\lambda=0.5nm=0.5(10)^(-9)m`

`E=((4.136(10)^(-15) eV.s)(3(10)^(8)m/s))/(0.5(10)^(-9)m)`

`E=(1.24(10)^(-6)eV.m )/(0.5(10)^(-9)m)`

`E=2480 eV`

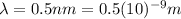
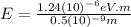
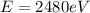
As we can see, as the wavelength decreases, the energy increases.