Hello!
The answer is:
The first triangle is:
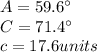
The second triangle is:
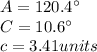
Why?
To solve the triangles, we must remember the Law of Sines form.
Law of Sines can be expressed by the following relationship:
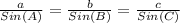
Where,
a, b, and c are sides of the triangle
A, B, and C are angles of the triangle.
We are given,
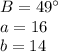
So, solving the triangles, we have:
- First Triangle:
Finding A, we have:
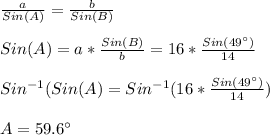
Finding C, we have:
Now, if the sum of all the interior angles of a triangle is equal to 180°, we have:
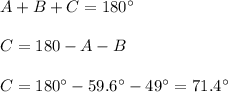
Finding c, we have:
Then, now that we know C, we need to look for "c":
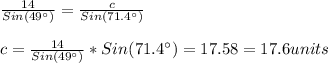
So, the first triangle is:
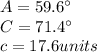
- Second Triangle:
Finding A, we have:
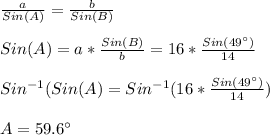
Now, since that there are two triangles that can be formed, (angle and its suplementary angle) there are two possible values for A, and we have:
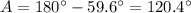
Finding C, we have:
Then, if the sum of all the interior angles of a triangle is equal to 180°, we have:
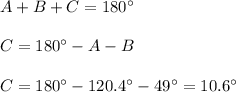
Then, now that we know C, we need to look for "c".
Finding c, we have:
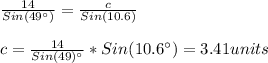
so, The second triangle is:
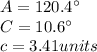
Have a nice day!