Question

Two triangles can be formed with the given information. Use the Law of Sines to solve the triangles.

B = 49°, a = 16, b = 14

Answer 1

Hello!

The answer is:

The first triangle is:

`A=59.6\°\\C=71.4\°\\c=17.6units`

The second triangle is:

`A=120.4\°\\C=10.6\°\\c=3.41units`

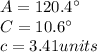
Why?

To solve the triangles, we must remember the Law of Sines form.

Law of Sines can be expressed by the following relationship:

`(a)/(Sin(A))=(b)/(Sin(B))=(c)/(Sin(C))`

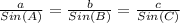
Where,

a, b, and c are sides of the triangle

A, B, and C are angles of the triangle.

We are given,

`B=49\°\\a=16\\b=14`

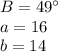
So, solving the triangles, we have:

- First Triangle:

Finding A, we have:

`(a)/(Sin(A))=(b)/(Sin(B))\\\\Sin(A)=a*(Sin(B))/(b)=16*(Sin(49\°))/(14)\\\\Sin^(-1)(Sin(A)=Sin^(-1)(16*(Sin(49\°))/(14))\\\\A=59.6\°`

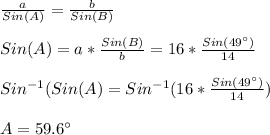
Finding C, we have:

Now, if the sum of all the interior angles of a triangle is equal to 180°, we have:

`A+B+C=180\°\\\\C=180-A-B\\\\C=180\°-59.6\°-49\°=71.4\°`

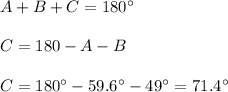
Finding c, we have:

Then, now that we know C, we need to look for "c":

`(14)/(Sin(49\°))=(c)/(Sin(71.4\°))\\\\c=(14)/(Sin(49\°))*Sin(71.4\°)=17.58=17.6units`

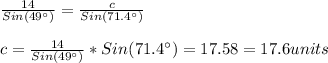
So, the first triangle is:

`A=59.6\°\\C=71.4\°\\c=17.6units`

- Second Triangle:

Finding A, we have:

`(a)/(Sin(A))=(b)/(Sin(B))\\\\Sin(A)=a*(Sin(B))/(b)=16*(Sin(49\°))/(14)\\\\Sin^(-1)(Sin(A)=Sin^(-1)(16*(Sin(49\°))/(14))\\\\A=59.6\°`

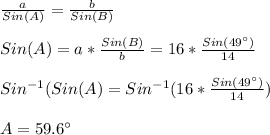
Now, since that there are two triangles that can be formed, (angle and its suplementary angle) there are two possible values for A, and we have:

`A=180\°-59.6\°=120.4\°`

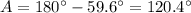
Finding C, we have:

Then, if the sum of all the interior angles of a triangle is equal to 180°, we have:

`A+B+C=180\°\\\\C=180\°-A-B\\\\C=180\°-120.4\°-49\°=10.6\°`

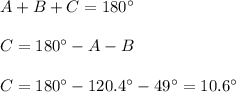
Then, now that we know C, we need to look for "c".

Finding c, we have:

`(14)/(Sin(49\°))=(c)/(Sin(10.6))\\\\c=(14)/(Sin(49)\°)*Sin(10.6\°)=3.41units`

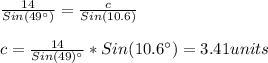
so, The second triangle is:

`A=120.4\°\\C=10.6\°\\c=3.41units`

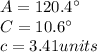
Have a nice day!