Answer:
The probability your mean age will be at least 28 is 83%
Explanation:
Let X denote the ages of all new employees hired during the last 10 years , then X is normally distributed with;
a mean of 31
a standard deviation of 10.
The sample size obtained is 10 employees. This implies that the sampling distribution of the sample mean will be normal with;
a mean of 31
a standard deviation of
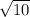
The sample mean is a statistic and thus has its own distribution. Its mean is equal to the population mean, 31 and its standard deviation is equal to
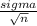
where sigma is the population standard deviation, 10 and n the sample size which in this case is 10.

We are required to find the probability that this sample mean age will be at least 28;
P(sample mean ≥ 28)
Since we know the distribution of the sample mean we simply standardize it to obtain the z-score associated with it;
P(sample mean ≥ 28)
=
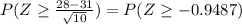
=0.8286
As a percentage this is equivalent to, 83%