Question

So, my buddy is new to doing Calculus and needs help understanding this equation, it would be very appeciated for some help

Answer 1

To evaluate the integral, rewrite the integrand as

`x^(-x)=e^{\ln x^(-x)}=e^(-x\ln x)`

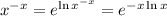
Recall that

`e^x=\displaystyle\sum_(n=0)^\infty(x^n)/(n!)\implies x^(-x)=\sum_(n=0)^\infty((-x\ln x)^n)/(n!)`

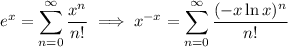
The leftmost sum is the well-known power series expansion for the function
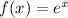`f(x)=e^x`. In the rightmost sum, we just replace
`x` with
`-x\ln x`.

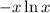This particular power series has a property called "uniform convergence". Roughly speaking, it's a property that says a sequence of functions
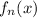`f_n(x)` converges to some limiting function
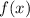`f(x)` in the sense that
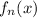`f_n(x)` and
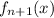`f_(n+1)(x)` get arbitrarily close to one another. If you have an idea of what "convergence" alone means, then you can think of "uniform convergence" as a more powerful form of convergence.

Long story short, this property allows us to interchange the order of summation/integration to write

`\displaystyle\int_0^1x^(-x)\,\mathrm dx=\int_0^1\sum_(n=0)^\infty((-x\ln x)^n)/(n!)\,\mathrm dx=\sum_(n=0)^\infty((-1)^n)/(n!)\int_0^1(x\ln x)^n\,\mathrm dx`

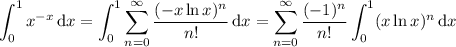
The integral can be tackled with a substitution,

`x=e^(-u/(n+1))\implies-(n+1)\ln x=u\implies\mathrm dx=-\frac1{n+1}e^(-u/(n+1))\,\mathrm du`

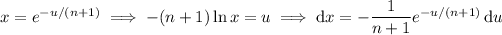
so that the integral is equivalent to

`\displaystyle\int_0^1(x\ln x)^n\,\mathrm dx=\int_\infty^0\left(e^(-u/(n+1))\right)^n\left(-\frac u{n+1}\right)^n\left(-\frac1{n+1}e^(-u/(n+1))\right)\,\mathrm du`

`=\displaystyle((-1)^n)/((n+1)^(n+1))\int_0^\infty e^(-u)u^n\,\mathrm du`

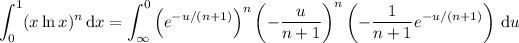
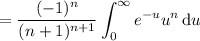
The remaining integral reduces to
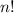`n!`, which you can derive for yourself via integration by parts/power reduction.

So we have

`\displaystyle\int_0^1x^(-x)\,\mathrm dx=\sum_(n=0)^\infty((-1)^n)/(n!)\cdot((-1)^nn!)/((n+1)^(n+1))=\sum_(n=0)^\infty\frac1{(n+1)^(n+1)}`

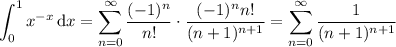
which is the same as

`\displaystyle\sum_(n=1)^\infty\frac1{n^n}=\sum_(n=1)^\infty n^(-n)`

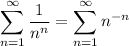
and hence the identity.