1 Answer

Casey Wilkins · Answer 1 · 2020-02-19T23:29:06+0000

Hello!

The answer is:

The rewritten expression is:

cos(2x)+sin(x)=(cos(x)+sin(x))*(cos(x)-sin(x))+sin(x)

To solve this problem we need to use the trigonometric identity of the double angle for the cosine which states that:

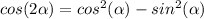
$cos(2\alpha)=cos^(2)(\alpha)-sin^(2)(\alpha)$

Also, if we want to rewrite only with terms of cos(x) and sin(x), we can apply the following property:

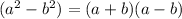
(a^(2) -b^(2))=(a+b)(a-b)

So, rewriting the trigonometric equation, we have:

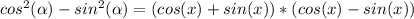
$cos^(2)(\alpha)-sin^(2)(\alpha)=(cos(x)+sin(x))*(cos(x)-sin(x))$

Then, we are given the expression:

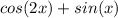
cos(2x)+sin(x)

Now, rewriting the given expression with only sin(x) and cos(x), we have:

cos(2x)+sin(x)=(cos(x)+sin(x))*(cos(x)-sin(x))+sin(x)

Hence, the answer is:

cos(2x)+sin(x)=(cos(x)+sin(x))*(cos(x)-sin(x))+sin(x)

Have a nice day!