Question

The vertex of this parabola is at (-5, -2). When the x-value is -4, the y-value is 2. What is the coefficient of the squared expression in the parabola equation?

Answer 1

The answer is 4

Explanation:

This is the correct answer

Answer 2

The coefficient of the squared expression in the parabola equation is
`a=4`

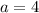
Explanation:

The equation of a parabola in its vertex form is:

`y = a(x-h) ^ 2 + k`

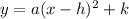
Where the vertex of the parabola is the point (h, k)

a is the ceoficiente of the term to the square.

We need to find the equation of a parabola that has its vertex in the point:

(-5, -2)

So:

`h = -5\\\\k = -2`

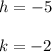
Therefore the equation is:

`y = a(x - (-5)) ^ 2 -2\\\\y = a(x + 5) ^ 2 -2`

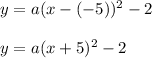
We know that the point (-4, 2) belongs to this parable. Then we can find the value of a by replacing the point in the equation of the parabola

`(2) = a((-4) + 5) ^ 2 -2\\\\2 = a(1) ^ 2 -2\\\\2 = a -2\\\\a = 4`

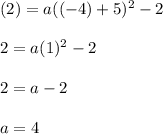
Finally the coefficient is a = 4