Answer:
P = 76%
Explanation:
We look for the percentage of employees who are at least 25 years old.
We know that:
μ = 32 years
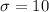 years
years
And we want to find
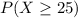
Then we find the z-score

So
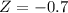
Then
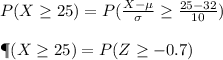
By symmetry of the distribution
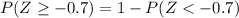
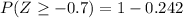
Looking in the normal standard tables
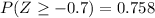
Finally P = 76%