Answer:
f(x) =
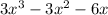
Explanation:
Which polynomial function has x intercepts -1,0, and 2 and passes through the point (1,-6)?
There are 3 distinct and real roots given in the question, which means that the function must be a third degree polynomial. The roots are -1, 0, and 2. This means that f(x) = 0 at these points. The general form of the cubic equation is given by:
f(x) = ax^3 + bx^2 + cx + d; where a, b, c, and d are arbitrary constants.
From the given data:
f(-1)=0 implies a*(-1)^3 + b*(-1)^2 + c(-1) + d = -a + b - c + d = 0. (Equation 1).
f(0)=0 implies a*(0)^3 + b*(0)^2 + c(0) + d = 0a + 0b + 0c + d = 0. (Equation 2).
f(2)=0 implies a*(2)^3 + b*(2)^2 + c(2) + d = 8a + 4b + 2c + d = 0. (Equation 3).
f(1)=0 implies a*(1)^3 + b*(1)^2 + c(1) + d = a + b + c + d = -6. (Equation 4).
Equation 2 shows that d = 0. So rest of the equations become:
-a + b - c = 0;
8a + 4b + 2c = 0; (Divide 2 on both sides of the equation to simplify).
a + b + c = -6
This system of equation can be solved using the Gaussian Elimination Method. Converting the system into the augmented matrix form:
• 1 1 1 | -6
• -1 1 -1 | 0
• 4 2 1 | 0
Adding row 1 into row 3:
• 1 1 1 | -6
• 0 2 0 | -6
• 4 2 1 | 0
Dividing row 2 with 2 and multiplying row 1 with -4 and add it into row 3:
• 1 1 1 | -6
• 0 1 0 | -3
• 0 -2 -3 | 24
Multiplying row 2 with 2 and add it into row 3:
• 1 1 1 | -6
• 0 1 0 | -3
• 0 0 -3 | 18
It can be seen that when this updated augmented matrix is converted into a system, it comes out to be:
• a + b + c = -6
• b = -3
• -3c = 18 (This implies that c = -6.)
Put c = -6 and b = -3 in equation 1:
• a + (-3) + (-6) = -6
• a = -6 + 3 + 6
• a = 3.
So f(x) =
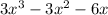(All conditions are being satisfied)!!!