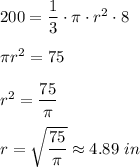Question

The tip of a solid metal cone was placed into a cube that has 10 inch edges, as shown.

If the water in the cube rose from 6 inches to 8 inches when the cone was placed in the cube, what is the
radius of the base of the submerged portion of the cone?

Answer 1

`r=\sqrt{(75)/(\pi)}\approx 4.89\ in`

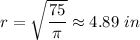
Explanation:

If the water in the cube rose from 6 inches to 8 inches when the cone was placed in the cube, then the difference in volumes is the volume of the submerged portion of the cone.

Initially, 10 in by 10 in by 6 in:

`V_(initial)=10\cdot 10\cdot 6=600\ in^2.`

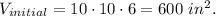
At he end, 10 in by 10 in by 8 in:

`V_(final)=10\cdot 10\cdot 8=800\ in^3.`

Thus,

`V_(submerged \ cone)=800-600=200\ in^3.`

Use cone's volume formula

`V_(cone)=(1)/(3)\pi r^2 \cdot h,`

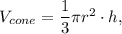
where r is the radius of the cone's base, h is the height of the cone.

From the diagram, h=8 in, then

`200=(1)/(3)\cdot \pi\cdot r^2\cdot 8\\ \\\pi r^2=75\\ \\r^2=(75)/(\pi)\\ \\r=\sqrt{(75)/(\pi)}\approx 4.89\ in`