Question

Determine whether each table below models a linear, quadratic or exponential function

Answer 1

Linear Quadratic Exponential

Explanation:

Answer 2

First table models Linear, second quadratic and third one exponential functions.

Explanation:

To find whether the given table models a linear function there should be a constant change in y values with the constant change in x values of the table.

We take the example of first table written as linear.

Here change in x values is

6 - 5 = 1

7 - 6 = 1

8 - 7 = 1

Similarly change in y values is

1 - 4 = -3

-2 - 1 = -3

-5 -(-2) = -3

There is a common difference in y values = -3

So the given table models linear function.

We take the second table.

For quadratic function with the constant change in x values, difference of difference in y values is constant.

Change in x - values

6 - 5 = 1

7 - 6 = 1

8 - 7 = 1

Difference in y values

1 - 0 = 1

4 - 1 = 3

9 - 4 = 5

Now difference in difference of y values

3 - 1 = 2

5 - 3 = 2

Here, difference in difference of y values is 2

So the given table models a quadratic equation.

Now we take the third table.

For exponential function in the form of
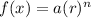`f(x) = a(r)^(n)` there should be a common ratio in the terms of y values.

`\frac{\text{Second term of y}}{\text{First term of y }}= (2)/(1)=2`

`\frac{\text{Third term of y}}{\text{Second term of y }}= (4)/(2)=2`

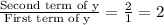
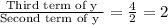
So there is a common ratio of 2 in each term.

Therefore, the given table models exponential equation.

First table models Linear, second quadratic and third one exponential functions.