Question

6.2 seconds The height, h, in feet of an object above the ground is given by h = −16t2 + 64t + 160, where t is the time in seconds. How long does it take the object to hit the ground? (to the nearest tenth of a second)

A)
5.1 seconds


B)
5.3 seconds


C)
5.7 seconds


D)
6.2 seconds

Answer 1

C) 5.7 seconds

Step-by-step explanation

The height of the object is given by:

`h(t) = - 16 {t}^(2) + 64t + 160`

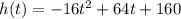
If the object hit the ground, then the height is zero.

`- 16 {t}^(2) + 64t + 160 = 0`

Divide through by -16

`{t}^(2) - 4t - 10 = 0`

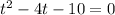
Where a=1, b=-4 and c=-10

We substitute into the quadratic formula to obtain,

`t= \frac{ - b \pm \sqrt{ {b}^(2) - 4ac} }{2a}`

`t= \frac{ - - 4\pm \sqrt{ {( - 4)}^(2) - 4( 1)( - 10)} }{2(1)}`

`t= ( 4\pm √(56) )/(2)`

`t= ( 4\pm 2√(14) )/(2)`

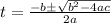
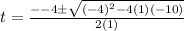
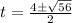
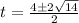
t=2-√14 or t=2+√14

Time cannot be negative.

Hence, t=5.7 seconds to the nearest tenth.