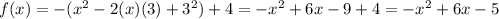Question

How do you do this problem

Answer 1

`\large\boxed{\text{Factored Form:}\ f(x)+-(x-1)(x-5)}\\\boxed{\text{Vertex Form:}\ f(x)=-(x-3)^2+4}\\\boxed{\text{Standard Form:}\ f(x)=-x^2+6x-5}`

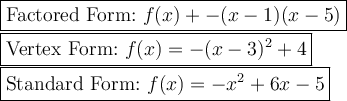
Explanation:

(look at the picture)

Factored form:

`f(x)=a(x-x_1)(x-x_2)`

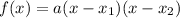
x₁, x₂ - zeros

Vertex form:

`f(x)=a(x-h)^2+k`

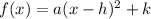
(h, k) - vertex

Standard form:

`f(x)=ax^2+bx+c`

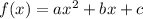
If from the vertex we go 1 unit down (up) and 1 unit left (right) and we get the point on the parabola, then a = 1.

The parabola is open down, therefore a < 0 → a = -1.

The zeros are
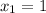`x_1=1` and
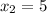`x_2=5`. Therefore the Factored Form is:

`f(x)=-(x-1)(x-5)`

The vertex is V(3, 4). Therefore the vertex form is:

`f(x)=-(x-3)^2+4`

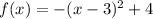
Convert it to a standard form using (a - b)² = a² - 2ab + b²

`f(x)=-(x^2-2(x)(3)+3^2)+4=-x^2+6x-9+4=-x^2+6x-5`