For this, let's go through each problem carefully and step-by-step.
According to the question, the rate of change of the temperature of any object that is defined by T, is directly proportional to the difference of T and the temperature of the environment around it, which we'll denote as X.
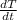
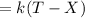
K is a constant of proportionality here. And the temperature of the surrounding environment is said to be (-18°C). Thus,
 .
.
For part A, in order to find the differential equation for T, we need to solve for k. So we separate the variables and then integrate to solve the equation.
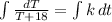
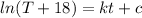
Now thw inital temperature of a pot of chili is 23°C, so at
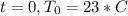 .
.
Substituting 23 for T and 0 for t, we have the following:
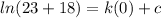
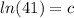
We know the temperature of chili after 2 hours is 7°C, so we know that when
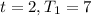
Substituting t for 2, and T for 7, we get:

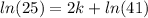
Solving for 2k
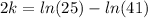
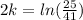
 .
.
Substituting the value of
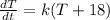 , the differential equation obtained is
, the differential equation obtained is
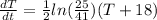 .
.
For part B, to find the temperature of the chili after four hours, we first need to solve the above differential equation.
The solution of the differential equation is given by the equation
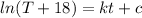 . Substituting the values of k and c, we have:
. Substituting the values of k and c, we have:
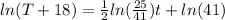 .
.
Using the above relation, at any time (t), the temperature (T) can be found out in the following.
At


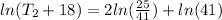
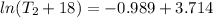
 ≅
≅
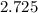
Solving the natural logarithm,
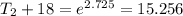
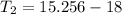
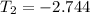 .
.
So the temperature of the chili after four hours would be -2.744°C approximately.
To find part C in what time the chili would be 10°C, we need to substitute again.
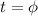
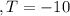
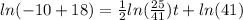
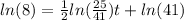
Solving for
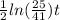 ,
,
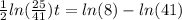

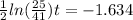
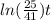

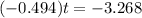
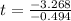
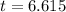 hours, approximately.
hours, approximately.
Thus, the chili would reach -10°C at around 6.615 hours.
Hope this helped. This took me a long time.