Answer:
WX (2,6) and (4,0)
TU (8,1) and (5,10)
Explanation:
We just need to calculate the slope of each of the possible answers and we'll know which is parallel. To be parallel, the other slope also has to be -3.
To calculate the slope, we do the difference of Y values over the difference X values.
WX (2,6) and (4,0)
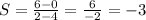
This slope is -3, so we have one right answer already, let's look for another.
PQ (5,6) and (8,7)
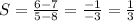
This is a perpendicular to MN, not a parallel.
RS (1,3) and (4,2)

Not parallel, nor perpendicular.
TU (8,1) and (5,10)
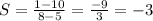
So, TU is also parallel to MN