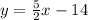Question

Write an equation for the line that is parallel to the given line and that passes through the given point. y = 5/2 x – 10; (–6, –29)

Answer 1

Answer:
`y=(5)/(2)x-14`

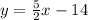
Explanation:

The equation of the line in slope-intercept form is:

`y=mx+b`

Where m is the slope and b the intersection with the y-axis.

You know the line
`y=(5)/(2)x-10`

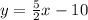
You can identify that:

`m=(5)/(2)`

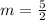
The slopes of Parallel lines are equal, then the slope of the other line is
`m=(5)/(2)`

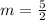
Substitute the slope and the given point into
`y=mx+b` and solve for b:

`-29=(5)/(2)(-6)+b\\-29=-15+b\\-29+15=b\\b=-14`

Substituting values, you get that the equation of this line is:

`y=(5)/(2)x-14`