Question

Finding the Vertex What is the vertex of the quadratic function f(x) = (x – 8)(x – 2)? (,)

Answer 1

Answer: (5,-9)

Explanation:

You need to apply Distributive property:

`f(x) = (x-8)(x-2)\\f(x)=x^2-2x-8x+16\\f(x)=x^2-10x+16`

Find the x-coordinate of the vertex with this formula:

`x=(-b)/(2a)`

In this case:

`b=-10\\a=1`

Then you get:

`x=(-(-10))/(2*1)=5`

Substitute x=5 into the function to find the y-coordinate:

`f(5)=y=5^2-10(5)+16=-9`

Therefore the vertex is: (5,-9)

Answer 2

(5, -9)

Explanation:

Let's multiply the function out:

f(x) = (x-8)(x-2)

`f(x)=x^2-2x-8x+16\\f(x)=x^2-10x+16`

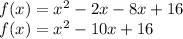
The vertex is (h, k), where

h = -b/2a

and

k is plugging in h into the equation

• a is the number before the x^2 term, hence a = 1
• b is the number before x term, hence b = -10
• c is the constant , hence c = 16

Plugging these into the formula for h, we get:

`h=-(b)/(2a)\\=-(-10)/(2(1))\\=5`

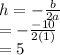
Now pluggin in 5 into the equation we get:

`x^2-10x+16\\(5)^2-10(5)+16\\=-9`

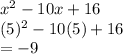
Hence, vertex is (5, -9)