Question

Which of the following would not be the result of a substitution in the following system? 2x + y = 7 y - x = 1

A) 7 - 2x - x = 1
B) 2x + x + 1 = 7
C) 2(y + 1) + y = 7

Answer 1

Answer: Option C.

Explanation:

A) The result of the substitution shown in Option A is obtained by solving for y from the first equation and substituting into the second equation:

`2x + y = 7\\y=7-2x`

`y - x = 1\\7-2x-x=1`

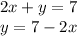
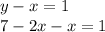
Therefore, this is a result of a substitution in the given system.

B) The result of the substitution shown in Option B is obtained by solving for y from the second equation and substituting into the first equation:

`y - x = 1`

`y=x+1`

`2x + y = 7\\2x + x + 1 = 7`

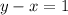
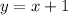
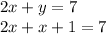
Therefore, this is a result of a substitution in the given system.

C) The result of the substitution shown in Option C is not a result of a substitution in the given system, because if you solve for x from the second equation and substitute into the first one, you get:

`y-x=1\\(-1)(-x)=(-y+1)(-1)\\x=y-1\\\\2(y - 1) + y = 7`