Question

Need help ASAP

1) A new truck that sells for $42,000 depreciates 11% each year. write a function that models the value of the truck. Find the value of the truck after 8 years. Round to the nearest dollar.

2) Earl mows lawns one weekend. He earns $15 for each lawn that he mows. He spends $50 on gas and other supplies. What function equation represents Earl's profit from mowing x lawns?

A)f(x)=50x-15
B)f(x)=50x+15
C)f(x)=15x-50
D)f(x)=15+50

3) find the common geometric series.
-2,-4,-8,-16.....

Answer 1

`\boxed{1) V = 40 000(0.89)^(n), \text{\$15 746; }\text{2) C) f(x) = 15x - 50 ; 3) }a_(n) = -2^(n)}`

Explanation:

1) Depreciation

The formula for the value V of an asset after depreciation by an annual percentage rate is

V = P(1 - r)ⁿ

where

P = present value

r = annual percentage rate

n = number of years

Data:

V = 40 000

r = 11 % = 0.11

n = 8 yr

Calculations:

(a) Function model

V= 40 000(1 - 0.11)ⁿ = 40 000(0.89)ⁿ

The function model is
`\boxed{ V= 40 000(0.89)^(n) }`

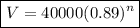
(b) Future value

V = 40 000(0.89)ⁿ = 40 000 × 0.393 659 = $15 746

In eight years, the truck will be worth
`\boxed{ \text{\$15 476}}.`

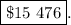
2) Profit function

Income from 1 lawn = $15

Income from x lawns = 15x

Less gas and supplies = -50

Net income = 15x – 50

The function is
`\boxed{f(x) = 15x - 50}`.

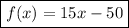3) Geometric series

(a) Calculate the common ratio

a₁ = -2

a₂ = -4

a₃ = -8

a₄ = =16

The ratios of consecutive pairs are

a₄/a₃ = -16/(-8) = 2

a₃/a₂ = -8/(-4) = 2

a₂/a₁ = -4/(-2) = 2

All adjacent pairs have the same common ratio r = 2.

(b) Write the formula for the series

The formula for the nth term of a geometric series is

aₙ = a₁rⁿ⁻¹

If a₁ = -2, the formula for the series is

aₙ = -2(2)ⁿ⁻¹ = -2ⁿ

The formula for the series is
`\boxed{a_(n) = -2^(n)}`.