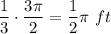I don't understand how to answer this

Question

asked Dec 4, 2020 111k views

1 Answer

Federico Jousset · Answer 1 · 2020-12-09T04:59:18+0000

Answer:

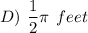
$\large\boxe{D)\ (1)/(2)\pi\ feet}$

Explanation:

Step 1:

Calculate the circumference of both circles.

The formula of a circumference:of a circle with radius r:

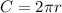
$C=2\pi r$

The circle R:

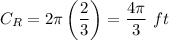
$C_R=2\pi\left((2)/(3)\right)=(4\pi)/(3)\ ft$

The circle S:

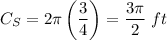
$C_S=2\pi\left((3)/(4)\right)=(3\pi)/(2)\ ft$

The length of the intercepted arc for circle R is

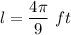
$l=(4\pi)/(9)\ ft$

Step 2:

Calculate what the part of the circumference of the circle R is the intercepted arc:

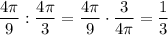
$(4\pi)/(9):(4\pi)/(3)=(4\pi)/(9)\cdot(3)/(4\pi)=(1)/(3)$

The same length of the circumference of the circle S is searched for the length of the intercepted arc for circle S.

Step 3:

Calculate the length of the intercepted arc for circle S:

$(1)/(3)\cdot(3\pi)/(2)=(1)/(2)\pi\ ft$