Answer:
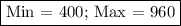
Explanation:
F = 8x + 5y
At (0, 100): F = 8×0 + 5×100 = 0 + 500 = 500
At (0, 80): F = 8×0 + 5×80 = 0 + 400 = 400 — MINIMUM
At (80, 60): F = 8×80 + 5×60 = 640 + 300 = 940
At (80, 0): F = 8×80 + 5×0 = 640 + 0 = 640
At (120, 0): F = 8×120 + 5×0 = 960 + 0 = 960 — MAXIMUM
The minimum value is
 and the maximum value is
and the maximum value is
 .
.