Answer:
option B
![\frac{280}{√(L)\sqrt[3]{P}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/t3s724dscosrcxcwki65x2xoyp46svp5gz.png)
Explanation:
Step 1
S varies inversely of the cube root of P
s
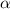
![\frac{1}{\sqrt[3]{P} }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dgip0lln7ajddpk696ul8buvnwhfdouowu.png)
s =
![\frac{k}{\sqrt[3]{P} }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3j9aq52r3prgr0ca507yt2qhn5s1pteufx.png)
Step 2
S varies inversely with square root of L
s
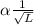
s =
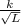
Step 3
Jointly
s =
![\frac{k}{√(L) \sqrt[3]{P} }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bgxqcaou83s9v0ggd19r12me7fq0jq0fpo.png)
Step 4
Plug values given in the question to find constant of proportionality
7 =
![\frac{k}{√(100)\sqrt[3]{64}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rx5j5b2vdg9gdizbeezcu8lqcyrdtrs8ru.png)
7 = k /(10)(4)
7 = k/40
k = 280
Step 5
General formula will be
s =
![\frac{280}{√(L)\sqrt[3]{P}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/t3s724dscosrcxcwki65x2xoyp46svp5gz.png)