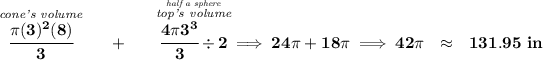Question

(I've been trying to figure this out for 3 days and I really need help)

1. You are opening a snow cone stand. Your cups, which are shaped like a cone, are 4" tall and have a 6" diameter. How much room is there in the cone without a top on the snow cone? (filled to the brim only)

2. The top of your snow cone is a perfect semicircle. It goes all the way across the cone. How many cubic inches of ice in the top of the snow cone?

3. How many cubic inches of snow cone will you be serving?

4.You want to start selling 2 different sizes of cones. You want your new cone to be twice as big as your current cone (top included). You found a cone that has a 6" diameter and is 8" tall. How many cubic inches of snow cone will you have with the new cone?

Answer 1

Check the picture below.

since the diameter of the cone is 6", then its radius is half that or 3", so getting the volume of only the cone, not the top.

1)

`\bf \textit{volume of a cone}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ r=3\\ h=4 \end{cases}\implies V=\cfrac{\pi (3)^2(4)}{3}\implies V=12\pi \implies V\approx 37.7`

2)

now, the top of it, as you notice in the picture, is a semicircle, whose radius is the same as the cone's, 3.

`\bf \textit{volume of a sphere}\\\\ V=\cfrac{4\pi r^3}{3}~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ r=3 \end{cases}\implies V=\cfrac{4\pi (3)^3}{3}\implies V=36\pi \\\\\\ \stackrel{\textit{half of that for a semisphere}}{V=18\pi }\implies V\approx 56.55`

3)

well, you'll be serving the cone and top combined, 12π + 18π = 30π or about 94.25 in³.

4)

pretty much the same thing, we get the volume of the cone and its top, add them up.

`\bf \stackrel{\textit{cone's volume}}{\cfrac{\pi (3)^2(8)}{3}}~~~~+~~~~\stackrel{\stackrel{\textit{half a sphere}}{\textit{top's volume}}}{\cfrac{4\pi 3^3}{3}/ 2}\implies 24\pi +18\pi \implies 42\pi ~~\approx~~131.95~in^`