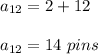Answer:
The explicit rule for this situation is
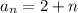
In row 12 there will be 14 pins
Explanation:
We have an initial amount of 3 pins in the first row. Let's call the number of pins in row n.
where n is an integer and
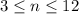 .
.
So
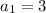
In row n + 1 there will always be a pin more than in the previous row n, then:
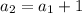
Then:
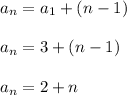
Finally in row 12 there will be: